1. What is dot prodcut?

The dot product is an algebraic operation that takes two same-sized vectors and returns a single number.

Algebraic definition
For two sequences of numbers, the dot product is the sum of the products of corresponding components of them. Think of two sequences $a$ and $b$ as below.

\[a = \begin{bmatrix} a_1 & a_2 & ... & a_n \end{bmatrix} \\ b = \begin{bmatrix} b_1 & b_2 & ... & b_n \end{bmatrix} \\\]

Then, the dot product of a and b becomes

\[a \cdot b = \sum_{i=1}^{n} a_i b_i\]

If $a$ and $b$ are row matrices, the dot product can be written as a matrix product. $a \cdot b = ab^\intercal$

For example, if $a = [a_1 \ a_2 \ a_3]$ and $b = [b_1 \ b_2 \ b_3]$, it becomes

\[[a_1 \ a_2 \ a_3] \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} =a_1b_1 + a_2b_2 + a_3b_3\]

Geometric definition
Geometrically, the dot product is the product of the Euclidean magnitudes of two vectors and the cosine of the angle between two.

\[a \cdot b = \vert a \vert \vert b \vert \rm cos \theta\]

Note that it is based on how much of one vector is in the direction of the other (projection). For example, in the below figure, the component of $A$ that is in the $B$ direction is $\vert A \vert \rm cos \theta$. Here, the magnitude of $A$ can be calculated by $\vert A \vert = \sqrt{x^2 + y^2}$ if $A = (x, y)$ and the initial point is the origin.

Fig 1. Projection of A onto B (Wikipedia)

Also note that if the two vectors are in the same direction, $\rm cos \theta = \rm cos 0^{\circ} = 1$ so it simply becomes the product of the magnitude of the two vectors, $a \cdot b = \vert a \vert \vert b \vert$. On the other hand, if the two vectors are perpendicular, the whole dot product becomes 0 because $\rm cos \theta = \rm cos 90^{\circ} = 0$.

Real world example
So what does the dot product really mean to us? How can we use it in the real life?
Imagine you are in a grocery store. You want to buy 1 apple, 2 oranges, and 3 bananas. The unit prices are \$1, \$2, \$0.5, respectively.

Fig 2. Apple, orange, and banana (image source)

You can define a number of items vector ($a$) and a unit price vector ($b$).

\[a = \begin{bmatrix}1 & 2 & 3 \end{bmatrix}\\ b = \begin{bmatrix}\$1 & \$2 & \$0.5\end{bmatrix}\\\]

The total cost will be the dot product of the two vectors:

\[ab^\intercal = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \begin{bmatrix} \$1 \\ \$2 \\ \$0.5 \end{bmatrix} =1 \times \$1 + 2 \times \$2 + 3 \times \$0.5 = \$6.5 \\\]

Ta-da! Your total is $6.5! Now we understand the dot product is something useful in our life, right?

2. What is matrix multiplication?

Now that we know what the dot product is, let’s talk about matrix multiplication. How is it different from dot product?

Matrix multiplication is basically a matrix version of the dot product. Remember the result of dot product is a scalar. The result of matrix multiplication is a matrix, whose elements are the dot products of pairs of vectors in each matrix.

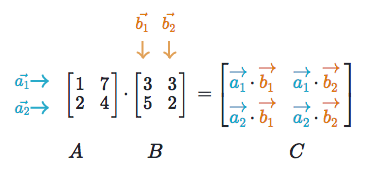
Fig 3. Matrix multiplication (image source)

Note that the number of columns in $A$ and the number of rows in $B$ should match; $A: (m \times n)$, $B: (n \times k) $.

Grocery example
Let’s go back to the previous grocery store example. Now there are two people who want to buy different numbers of apples, oranges, and bananas.

Person 1 wants 1 of each fruit: $a_1 = [1 \ \ 1 \ \ 1]$
Person 2 wants 10 of each fruit: $a_2 = [10 \ \ 10 \ \ 10]$

How much should each person pay? Can we repeat the dot product? Absolutely! But instead of doing the dot product twice, we can stack up the vectors to build a matrix and that’s simply the matrix multiplication!

The number of apples, oranges, and bananas to buy:

\[A= \begin{bmatrix} a_1\\ a_2 \end{bmatrix}= \begin{bmatrix} 1 & 1 & 1\\ 10 & 10 & 10\\ \end{bmatrix}\]

Now, for the unit price vector $b$, we need to transpose b to make it a column vector.

\[B = \begin{bmatrix} \$1\\ \$2\\ \$0.5 \end{bmatrix}\]

Now the total price each person has to pay is:

\[A \cdot B = \begin{bmatrix} 1 & 1 & 1\\ 10 & 10 & 10 \end{bmatrix} \begin{bmatrix} \$1\\ \$2\\ \$0.5 \end{bmatrix} = \begin{bmatrix} 1 \times \$1 + 1 \times \$2 + 1 \times \$0.5 \\ 10 \times \$1 + 10 \times \$2 + 10 \times \$0.5 \end{bmatrix} = \begin{bmatrix} \$3.5 \\ \$35 \end{bmatrix}\]

YAY ! With just one simple matrix multiplication, we came up with that person 1 should pay \$3.5 and person 2 should pay \$35! You will now use matrix multiplication when you go to a grocery shopping, right?